Gradient descent cho hàm nhiều biến - Code Python

 Problem:

Bài toán thực tế:

Một căn nhà rộng $x_1{\text{m}}^2$, có $x_2$ phòng ngủ và cách trung tâm thành phố $x_3\text{km}$ có giá là bao nhiêu. Giả sử chúng ta đã có số liệu thống kê từ 1000 căn nhà trong thành phố đó, liệu rằng khi có một căn nhà mới với các thông số về diện tích, số phòng ngủ và khoảng cách tới trung tâm, chúng ta có thể dự đoán được giá của căn nhà đó không?

Diễn dãi theo code:

h = so hang

c = so cot

Input:

    h, c

    x[1][1] ... x[h][c]

y[1] ... y[h]

    x[h+1][1] ... x[h+1][c]

Ouput:

    y[h+1]

Solve:

Ta co

θ[1] * x[1][1] + ...  + θ[c] * x[1][c] ~ y[1]

...

...

θ[1] * x[h][1] + ...  + θ[c] * x[h][c] ~ y[h]

=> θ[1]* x[h+1][1] + ...  + θ[c]*x[h+1][c] ~ y[h+1]

=> Can tim cac θ de giai quyet bai toan

Ví dụ đơn giản:

Input: Cho tập điểm (x, y)

Ouput: Tìm 1 đường thằng gần tất cả các điểm nhất (tìm a, b của đường thằng y= ax + b)

Solve:

B1: Dự đoán θ0, θ1 (~ a, b)

B2: Cập nhập θ cho đến khi đạt điều kiện dừng (thường  abs(dHMM) < epsilon, loop = ...)

              θ_new = θ_old  - alpha * dHMM

  Cách tìm θi của bài toán trên 

Code Python:

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(2)

def grad(w):

    N = Xbar.shape[0]

    return 1/N * Xbar.T.dot(Xbar.dot(w) - y)

def l(w):

    N = Xbar.shape[0]

    return .5/N*np.linalg.norm(Xbar.dot(w)-y, 2)**2

def myGradientDescent(w_init, grad, alpha, loop = 1000, esilon = 1e-4):

    w = [w_init]

    for i in range(loop):

        w_new = w[-1] - alpha*grad(w[-1])

        if np.linalg.norm(grad(w_new))/len(w_new) < esilon:

            break

        w.append(w_new)

    return (w, i)

if __name__ == '__main__':

    # dataset

    X = np.random.rand(1000, 1)

    y = 4 + 3 * X + .2 * np.random.randn(1000, 1)  # noise added

    # Building Xbar

    one = np.ones((X.shape[0], 1))

    Xbar = np.concatenate((one, X), axis=1)

    # Gradient descent

    w_init = np.array([[2], [1]])

    (w1, it1) = myGradientDescent(w_init, grad, 1)

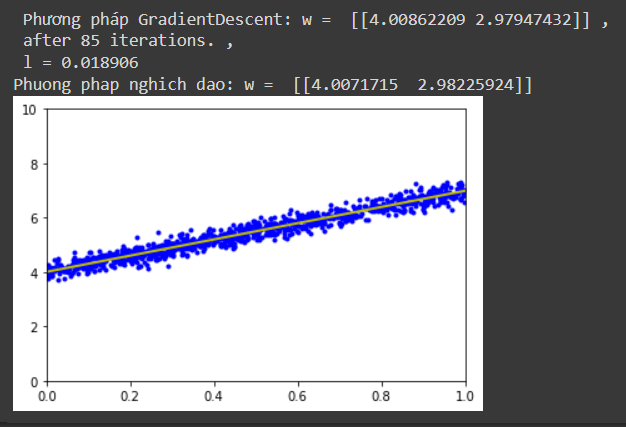
    print(' Phương pháp GradientDescent: w = ', w1[-1].T, ',\n after %d iterations.' %(it1+1),',\n l = %f ' % l(w1[-1]))

    # Linear regression

    A = np.dot(Xbar.T, Xbar)

    b = np.dot(Xbar.T, y)

    w_lr = np.dot(np.linalg.pinv(A), b)

    print('Phuong phap nghich dao: w = ', w_lr.T)

    # Display result

    w = w_lr

    w_0 = w[0][0]

    w_1 = w[1][0]

    x0 = np.linspace(0, 1, 2, endpoint=True)

    y0 = w_0 + w_1 * x0

   

    # Draw the fitting line

    plt.plot(X.T, y.T, 'b.')  # data

    plt.plot(x0, y0, 'y', linewidth=2)  # the fitting line

    plt.axis([0, 1, 0, 10])

    plt.show()

Ouput:

Các nguồn tham khảo: Link1, Link2

Xem thêm bài viết cùng chủ đề: Gradient Descent cho hàm 1 biến